Penjelasan Lengkap Mengenai Jaring Jaring Kerucut dalam Dunia Pendidikan

Apa yang terlintas dalam pikiran Anda ketika mendengar kata “jaring-jaring kerucut”? Mungkin sebagian besar dari kita akan langsung terbayang dengan bentuk tali yang saling terhubung membentuk rangkaian yang rumit dan kompleks. Namun, tahukah Anda bahwa jaring-jaring kerucut juga memiliki peran penting dalam dunia pendidikan?

Pengertian Jaring Jaring Kerucut

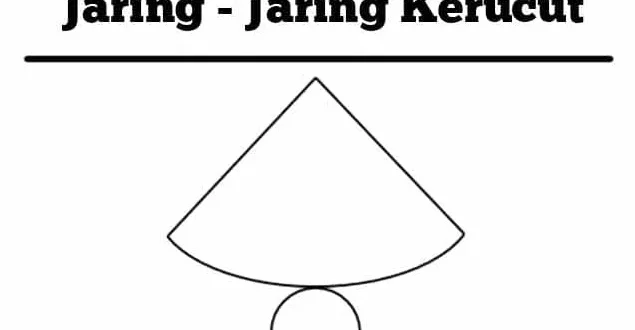
Jaring jaring kerucut adalah suatu pola dua dimensi yang dibuat dengan menghubungkan semua titik yang terletak pada permukaan sebuah kerucut. Jaring jaring ini terdiri dari sejumlah segitiga yang membentuk wajah-wajah kerucut tersebut. Dengan adanya jaring jaring kerucut, kita dapat memvisualisasikan bagaimana permukaan kerucut terbentuk secara lebih jelas.

Definisi Jaring Jaring Kerucut

Jaring jaring kerucut dapat didefinisikan sebagai kumpulan segitiga yang membentuk rangkaian pola pada permukaan kerucut. Segitiga-segitiga ini menghubungkan semua titik yang terdapat pada permukaan kerucut, sehingga membentuk suatu jaring jaring yang terdiri dari garis-garis penghubung antar titik.

Elemen-Elemen Jaring Jaring Kerucut

Jaring jaring kerucut terdiri dari elemen-elemen berikut:

1. Segitiga: Segitiga merupakan elemen dasar yang membentuk jaring jaring kerucut. Setiap segitiga terdiri dari tiga titik pada permukaan kerucut yang dihubungkan oleh garis. Kumpulan segitiga ini akan membentuk pola tertentu sesuai dengan bentuk kerucut yang diinginkan.

2. Titik-titik: Selain segitiga, terdapat juga titik-titik yang terdapat pada permukaan kerucut. Titik-titik ini merupakan titik potong antara garis-garis penghubung segitiga-segitiga yang membentuk jaring jaring kerucut.

3. Garis: Garis-garis ini merupakan penghubung antar titik pada permukaan kerucut. Setiap garis menghubungkan dua titik atau lebih, dengan tujuan membentuk pola jaring jaring yang terdiri dari segitiga-segitiga.

Bentuk-Bentuk Jaring Jaring Kerucut

Ada beberapa bentuk jaring jaring kerucut yang berbeda, di antaranya:

1. Kerucut Biasa: Ini adalah bentuk jaring jaring kerucut paling sederhana, di mana segitiga-segitiga membentuk pola yang merata dan tidak ada perubahan ukuran pada wajah-wajah kerucut.

2. Kerucut Terpancung: Pada bentuk ini, segitiga-segitiga yang membentuk jaring jaring kerucut lebih tajam dan rapat di bagian atas kerucut, namun semakin menjauh dari puncak, segitiga-segitiga tersebut semakin melebar.

3. Kerucut Terbentur: Bentuk ini memiliki pola segitiga-segitiga yang tidak merata dan terdapat perubahan ukuran pada wajah-wajah kerucut. Hal ini terjadi karena adanya guncangan atau benturan ketika kerucut terbentuk.

Dengan memahami elemen-elemen dan bentuk-bentuk jaring jaring kerucut, kita dapat mengaplikasikannya dalam berbagai konteks, seperti dalam matematika, arsitektur, dan ilmu fisika. Penggunaan jaring jaring kerucut ini bisa memberikan gambaran yang lebih jelas dan detail tentang struktur dan karakteristik kerucut secara keseluruhan.

Kegunaan Jaring Jaring Kerucut dalam Matematika

Jaring jaring kerucut memiliki beberapa kegunaan penting dalam matematika. Salah satunya adalah untuk menghitung luas permukaan kerucut. Dalam menghitung luas permukaan kerucut, kita menggunakan jaring jaring kerucut dengan cara mengukur luas total dari semua segitiga yang membentuk jaring jaring tersebut. Dengan mengetahui luas permukaan kerucut, kita dapat menentukan berapa banyak bahan yang diperlukan untuk melapisinya, misalnya saat membuat topi kerucut atau melakukan perancangan struktur bangunan yang memiliki bentuk kerucut.

Menghitung Luas Permukaan Kerucut

Untuk menghitung luas permukaan kerucut, kita perlu mengukur luas dari setiap segitiga yang membentuk jaring jaring kerucut. Jaring jaring kerucut sendiri terdiri dari banyak segitiga-sesgitiga yang terhubung dan membentuk permukaan kerucut. Luas setiap segitiga ini dapat dihitung dengan menggunakan rumus luas segitiga, yaitu 1/2 x alas x tinggi. Setelah mendapatkan luas setiap segitiga, kita dapat menjumlahkannya untuk mendapatkan luas permukaan kerucut secara keseluruhan.

Contoh penghitungan luas permukaan kerucut:

1. Misalkan jari-jari kerucut adalah r dan garis pelukisnya adalah s.

2. Maka tinggi kerucut (tinggi jaring jaring) adalah √(s^2 – r^2), dengan menggunakan teorema Pythagoras.

3. Setelah mengetahui tinggi kerucut, kita dapat menghitung luas setiap segitiga yang membentuk jaring jaring kerucut.

4. Luas setiap segitiga = 1/2 x alas (jarak dua titik di sekeliling jaring jaring) x tinggi (tinggi kerucut).

5. Jumlahkan luas setiap segitiga untuk mendapatkan luas permukaan kerucut secara keseluruhan.

Dengan menggunakan jaring jaring kerucut dalam menghitung luas permukaan, kita dapat menghemat waktu dan usaha dalam mengukur ketelitian luas permukaan kerucut. Selain itu, penggunaan jaring jaring kerucut juga memudahkan kita dalam menggambarkan dan memvisualisasikan bentuk kerucut secara lebih akurat.

Menghitung Volume Kerucut

Selain dapat digunakan untuk menghitung luas permukaan, jaring jaring kerucut juga dapat digunakan untuk menghitung volume kerucut. Volume kerucut adalah ukuran ruang yang terkurung di dalam jaring jaring kerucut. Untuk menghitung volume kerucut, kita dapat menggunakan rumus yang berbeda tergantung pada bentuk kerucut yang dimiliki.

Contoh penghitungan volume kerucut:

1. Misalkan jari-jari kerucut adalah r dan tinggi kerucut adalah t.

2. Dengan menggunakan rumus volume kerucut (1/3 x luas alas x tinggi), kita dapat menghitung luas alas kerucut menggunakan rumus luas lingkaran (π x r^2) dan mendapatkan volume kerucut secara keseluruhan.

Penggunaan jaring jaring kerucut dalam menghitung volume kerucut memungkinkan kita untuk menentukan berapa banyak ruang yang dapat diisi oleh suatu objek yang memiliki bentuk kerucut. Hal ini sangat berguna dalam perancangan struktur bangunan yang membutuhkan perhitungan volume secara presisi, seperti kubah atau kerucut gelas.

Penerapan dalam Kehidupan Sehari-hari

Penerapan jaring jaring kerucut dalam kehidupan sehari-hari sangatlah luas. Salah satunya adalah dalam perancangan bangunan atau struktur yang memiliki bentuk kerucut. Bangunan seperti kubah, taman bermain, dan kerucut gelas merupakan contoh-contoh bentuk yang menggunakan prinsip dasar jaring jaring kerucut.

Bangunan kubah menggunakan jaring jaring kerucut dalam merancang konstruksi atapnya. Dengan menggunakan jaring jaring kerucut, para arsitek dapat menentukan dimensi dan ukuran yang tepat untuk konstruksi atap kubah sehingga memiliki daya tahan struktural yang baik dan efisiensi yang maksimal.

Taman bermain sering kali memiliki permainan seperti taman seluncur atau permainan air dengan bentuk kerucut. Penggunaan jaring jaring kerucut pada permainan ini memungkinkan anak-anak untuk menjalani pengalaman bermain yang menyenangkan sambil tetap memiliki faktor keamanan yang terjamin.

Kerucut gelas adalah bentuk umum dalam kehidupan sehari-hari. Jaring jaring kerucut dapat digunakan untuk merancang bentuk kerucut gelas yang menarik dan fungsional. Dengan menggunakan pengetahuan tentang luas permukaan dan volume kerucut, desainer gelas dapat menciptakan produk yang memiliki estetika menarik dan kapasitas volume yang tepat.

Dalam kesimpulannya, jaring jaring kerucut memiliki banyak kegunaan dalam matematika, termasuk dalam menghitung luas permukaan dan volume kerucut. Selain itu, penerapan jaring jaring kerucut dalam kehidupan sehari-hari seperti dalam perancangan bangunan atau struktur yang memiliki bentuk kerucut juga sangat umum. Dengan pemahaman yang baik tentang jaring jaring kerucut, kita dapat lebih menghargai keindahan dan kemampuan matematika yang terkandung dalam bentuk-bentuk kerucut di sekitar kita.