Rumus Volume Kerucut

Selamat datang di artikel “Rumus Volume Kerucut”! Kami akan membahas segala hal yang perlu Anda ketahui tentang kerucut, termasuk bentuk, sifat-sifatnya, dan bagaimana menghitung volume kerucut. Mari kita mulai!

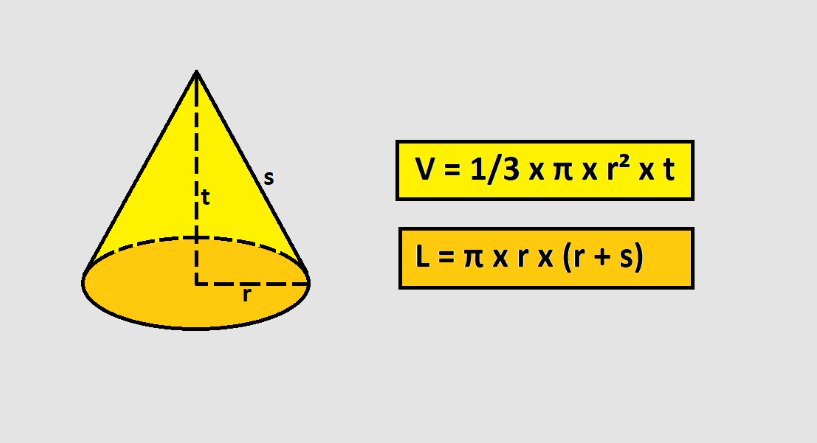
Mengenal Kerucut: Bentuk dan Sifat-Sifatnya

Kerucut adalah salah satu bentuk geometri tiga dimensi yang memiliki ciri khas, yaitu bentuk yang mirip dengan topi es krim atau tumpukan cangkir. Kerucut memiliki dua sisi yang penting: alas dan pelukis (atau tepi). Alasnya adalah lingkaran yang terletak di bawah kerucut, sedangkan pelukis adalah permukaan lengkung yang menghubungkan alas dengan titik puncak kerucut.

Sifat-sifat penting kerucut meliputi tinggi, jari-jari alas, dan garis pelukis. Tinggi kerucut adalah jarak vertikal dari puncak kerucut hingga alasnya. Jari-jari alas adalah jarak dari pusat lingkaran alas ke tepi lingkaran. Garis pelukis adalah panjang garis yang menghubungkan titik puncak kerucut dengan tepi lingkaran alas.

Untuk menghitung volume kerucut, kita perlu memahami sifat-sifat ini dan bagaimana mereka berhubungan satu sama lain.

Dasar-Dasar Perhitungan Volume Kerucut

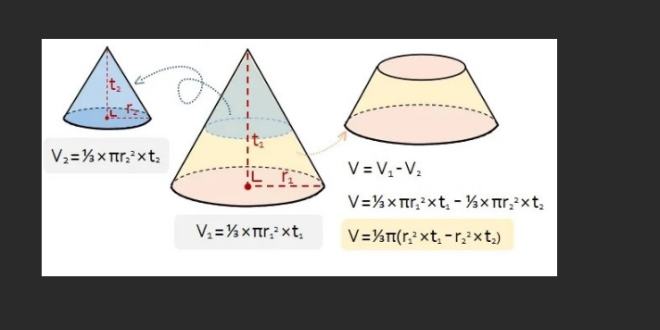
Perhitungan volume kerucut didasarkan pada prinsip dasar geometri. Rumus volume kerucut adalah:

Volume = (1/3) x π x r² x h

Di mana:

• Volume adalah volume kerucut.
• π (Pi) adalah konstanta matematika yang kurang lebih 3.14159.
• r adalah jari-jari alas kerucut.
• h adalah tinggi kerucut.

Rumus ini akan membantu Anda menghitung volume kerucut dengan tepat. Selanjutnya, mari kita bahas lebih dalam tentang rumus ini.

Rumus Dasar Volume Kerucut

Rumus dasar volume kerucut yang disebutkan di atas adalah inti dari perhitungan volume kerucut. Dengan rumus ini, Anda dapat menghitung volume kerucut dengan mudah.

Volume kerucut dihitung dengan mengalikan setengah dari luas alas (π x r²) dengan tinggi kerucut (h). Hasilnya kemudian dibagi oleh tiga untuk mendapatkan volume kerucut. Rumus ini sangat penting karena dapat diterapkan pada berbagai situasi yang melibatkan kerucut, seperti menghitung volume wadah, kerucut lalu lintas, atau bahkan produk-produk yang memiliki bentuk kerucut.

Jadi, jika Anda ingin menghitung volume kerucut, cukup masukkan nilai jari-jari alas (r) dan tinggi (h) ke dalam rumus, lalu hitung hasilnya. Rumus ini sangat sederhana, dan dengan menggunakan kalkulator atau perangkat hitung, perhitungan volume kerucut dapat dilakukan dengan cepat dan akurat.

Menghitung Volume Kerucut dengan Jari-Jari dan Tinggi

Untuk menghitung volume kerucut, langkah pertama yang perlu Anda lakukan adalah mengukur jari-jari alas (r) dan tinggi (h) kerucut. Jari-jari alas adalah jarak dari pusat lingkaran alas ke tepi lingkaran, sedangkan tinggi adalah jarak vertikal dari puncak kerucut ke alasnya.

Setelah Anda memiliki nilai r dan h, Anda bisa langsung menghitung volume kerucut menggunakan rumus dasar yang telah dijelaskan sebelumnya:

Volume = (1/3) x π x r² x h

Masukkan nilai r dan h ke dalam rumus, dan lakukan perhitungan. Hasilnya adalah volume kerucut dalam satuan kubik (misalnya, cm³ atau m³).

Sebagai contoh, mari kita ambil kasus sederhana. Misalkan jari-jari alas kerucut adalah 5 cm dan tingginya adalah 12 cm. Bagaimana kita menghitung volumenya?

Volume = (1/3) x π x (5 cm)² x 12 cm = (1/3) x π x 25 cm² x 12 cm = (1/3) x π x 300 cm³ = 100π cm³

Jadi, volume kerucut dalam kasus ini adalah 100π cm³. Jika Anda ingin menghitung nilai numeriknya, Anda bisa menggunakan perkiraan π sekitar 3.14159, sehingga volume kerucut adalah sekitar 314.16 cm³.

Sekarang Anda tahu cara menghitung volume kerucut dengan mudah!

Aplikasi Rumus Volume Kerucut dalam Kehidupan Sehari-Hari

Rumus volume kerucut mungkin terdengar seperti konsep matematika abstrak yang sulit diterapkan dalam kehidupan sehari-hari, tetapi sebenarnya, kita sering menggunakan konsep ini tanpa menyadarinya. Berikut beberapa contoh bagaimana rumus volume kerucut dapat digunakan dalam situasi nyata:

1. Wadah Minuman: Botol minuman sering memiliki bentuk kerucut terbalik. Dengan mengetahui volume wadah, produsen dapat menghitung berapa banyak cairan yang dapat disimpan dalam botol tersebut.

2. Lalu Lintas: Lampu lalu lintas kerucut digunakan di

banyak persimpangan. Volume kerucut dapat membantu para insinyur lalu lintas menghitung berapa banyak bahan yang diperlukan untuk membuat lampu lalu lintas tersebut.

3. Kerucut Es Krim: Kerucut es krim adalah salah satu contoh penerapan yang lebih jelas. Rumus volume kerucut digunakan untuk menghitung berapa banyak es krim yang dapat diisi ke dalam sebuah kerucut es krim.

4. Kendaraan: Knalpot kendaraan sering memiliki bentuk kerucut pada ujungnya. Pabrikan kendaraan dapat menggunakan rumus volume kerucut untuk mendesain knalpot agar dapat mengatur emisi gas buang secara efisien.

5. Industri Kimia: Dalam industri kimia, kerucut sering digunakan dalam tangki penyimpanan dan reaktor. Perhitungan volume kerucut sangat penting untuk mengukur jumlah bahan kimia yang disimpan atau reaksi kimia yang terjadi dalam tangki tersebut.

Jadi, meskipun rumus volume kerucut mungkin terlihat seperti konsep matematika murni, aplikasinya sangat relevan dalam berbagai aspek kehidupan sehari-hari.

Volume Kerucut: Contoh Perhitungan Sederhana

Untuk memahami lebih jelas bagaimana rumus volume kerucut digunakan dalam situasi nyata, mari kita lihat beberapa contoh perhitungan sederhana.

Contoh 1: Botol Minuman

Bayangkan Anda bekerja di pabrik minuman dan Anda bertugas untuk mengisi botol minuman dengan bentuk kerucut terbalik. Anda diberikan tugas menghitung berapa banyak cairan yang dapat muat dalam botol tersebut. Botol memiliki jari-jari alas sebesar 4 cm dan tingginya adalah 15 cm. Bagaimana Anda menghitung volumenya?

Volume = (1/3) x π x (4 cm)² x 15 cm = (1/3) x π x 16 cm² x 15 cm = (1/3) x π x 240 cm³ = 80π cm³

Jadi, volume botol minuman adalah 80π cm³. Jika Anda ingin menghitung nilai numeriknya, Anda bisa menggunakan perkiraan π sekitar 3.14159, sehingga volume botol minuman adalah sekitar 251.2 cm³.

Contoh 2: Lampu Lalu Lintas

Seorang insinyur lalu lintas sedang merancang lampu lalu lintas dengan bentuk kerucut pada ujungnya. Lampu tersebut memiliki jari-jari alas sebesar 6 cm dan tingginya adalah 20 cm. Berapa volume lampu lalu lintas tersebut?

Volume = (1/3) x π x (6 cm)² x 20 cm = (1/3) x π x 36 cm² x 20 cm = (1/3) x π x 720 cm³ = 240π cm³

Jadi, volume lampu lalu lintas adalah 240π cm³. Dengan perkiraan π sekitar 3.14159, volume lampu lalu lintas adalah sekitar 753.6 cm³.

Contoh 3: Kerucut Es Krim

Seorang penjual es krim ingin menghitung berapa banyak es krim yang dapat diisi ke dalam kerucut es krim. Kerucut es krim tersebut memiliki jari-jari alas sebesar 8 cm dan tingginya adalah 12 cm. Bagaimana cara menghitung volumenya?

Volume = (1/3) x π x (8 cm)² x 12 cm = (1/3) x π x 64 cm² x 12 cm = (1/3) x π x 768 cm³ = 256π cm³

Jadi, volume kerucut es krim adalah 256π cm³. Dengan perkiraan π sekitar 3.14159, volume kerucut es krim adalah sekitar 804.8 cm³.

Semua contoh di atas menunjukkan bagaimana rumus volume kerucut dapat digunakan untuk menghitung volume berbagai objek dalam kehidupan sehari-hari. Selanjutnya, kita akan membahas beberapa rumus alternatif yang dapat digunakan untuk menghitung volume kerucut.

Rumus Alternatif untuk Menghitung Volume Kerucut

Di samping rumus dasar volume kerucut yang telah kita pelajari, ada beberapa rumus alternatif yang dapat digunakan tergantung pada informasi yang tersedia. Dua rumus alternatif yang sering digunakan adalah:

Rumus 1: Volume = (1/3) x π x r² x H

Di sini, H adalah tinggi pelukis kerucut. Jika Anda memiliki nilai H dan jari-jari alas (r), Anda dapat menggunakan rumus ini untuk menghitung volume kerucut.

Rumus 2: Volume = (1/3) x A x h

Di sini, A adalah luas alas kerucut. Jika Anda memiliki nilai luas alas (A) dan tinggi (h), Anda dapat menggunakan rumus ini untuk menghitung volume kerucut.

Salah satu keuntungan menggunakan rumus alternatif adalah ketika Anda memiliki data yang tidak mencakup jari-jari alas dan tinggi secara langsung. Misalnya, jika Anda hanya memiliki tinggi pelukis dan tinggi, Anda dapat menggunakan Rumus 1 untuk menghitung volume. Begitu juga jika Anda hanya memiliki luas alas dan tinggi, Anda dapat menggunakan Rumus 2.